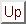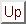
Turbulence causes large variations in point and line-averaged wind measurements. These variations often dominate the difference between traditional measurements and the VIL observations. Therefore, the point and line-averaged measurements are not referenced when analyzing the accuracy of the wind profiling method. Calculated error estimates of the VIL wind profiles are compared with the local consistency of the measurements. The local consistency is calculated for each wind measurement by subtracting the average of its vertically adjacent wind measurements. If the vertical wind shear is linear, the variations between adjacent vertical values presents the measurement inaccuracy.
The Cartesian mapping procedure introduced in Section 4.1.2
may cause profile smoothing by mixing the aerosols from
different layers.
Therefore, the Cartesian mapping routine is slightly modified for
the consistency analysis:
each backscatter signal element is averaged into the closest
grid point instead of dividing it into the eight closest grid points.
Also, the filling of the empty pixels is performed only in xy-plane.
This eliminates the vertical mixing of the CAPPI scans
due to the mapping algorithm.
Data from July 26, 1989, is selected (see Figure 35) for accuracy
calculations, since the wind shear is more linear on that day than
on any other day in the FIFE program.
The same case was also analyzed with the original cartesian mapper.
The maximum difference between the wind results calculated from differently
mapped CAPPI scans is about 0.1 ms
in speed and 0.5
in direction.
The RMS errors were smaller for the original
Cartesian mapper, indicating the noise in the CCF planes was also smaller
because of more efficient averaging.
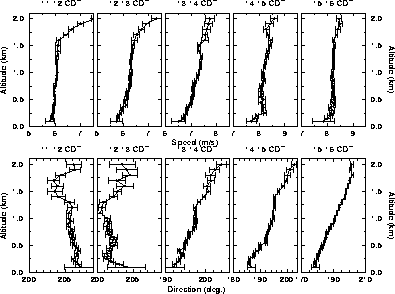
Figure 35:
Hourly averaged wind profiles on July 26, 1989, between
11:00 and 16:00 CDT.
Only results with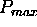 
= 1 are plotted.
The mixed layer mean depth rises rapidly to 1000 m
before 11:00 CDT when the clouds start forming.
The base of convective clouds varies between 1000 m and
1800 m during the
measurement period.
The wind speed shear is linear except in the first 200-300 meters
and at the top of the CBL.
Error bars show estimated root-mean-square errors.
Figure 36 compares the local deviations and calculated RMS error estimates for hourly averaged wind profiles on July 26, 1989. The local deviations are calculated from the averages of vertically adjacent results. The calculated error estimates represent RMS errors in wind determination from noise in the CCF
after the wind estimates with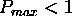 
are rejected.
The calculated RMS error estimates are consistent with
the internal consistency of the results.
In the convective boundary layer (below 1400 m),
the local deviations are less than 0.1 ms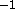
in speed and
1
in direction.
Part of the local variation is probably due to real wind fluctuations.
Thus, it may provide a conservative estimate of the accurasy.
The calculated profiles show minimum RMS errors at about 1 km:
the contrast between scattering from aerosol structures and
mixed air is very good just below the CBL top, since
the clear air penetrating down to the CBL is not yet
mixed with the boundary layer aerosols.
Closer to the ground, more intense mixing smears the aerosol
structures, decreasing the signal-to-noise ratio of the CCF
and flattening the CCF peak.
Above the convective boundary layer, clouds block the signal
decreasing the signal-to-noise ratio.
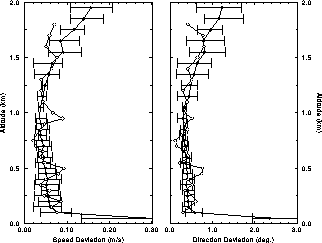
Figure 36:
Local deviations of hourly averaged wind speed and direction (open circles)
and calculated RMS error estimates (black circles) on July 26, 1989,
between 11:00 and 16:00 CDT.
The error bars indicate the minimum and maximum error of
hourly averaged wind estimates during the 5-hour observation session.
The calculated error estimates are consistent with
the local deviations.
Figure 37 shows calculated
RMS error estimates of wind measurements
as functions of the averaged time and normalized altitude
from July 26 to July 31, 1989.
Error estimates are first linearly interpolated into altitudes normalized
by the convective boundary layer mean depths and then averaged over time.
In the CBL, the error estimates are almost constant with altitude;
above the CBL, they grow almost exponentially.
In the convective boundary layer,
the RMS errors are on the average less than 0.2 ms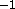
in speed
and 3.0
in direction.
In the middle of the convective boundary layer,
where aerosol structures have good contrast against the background,
the RMS errors are 0.03--0.05 ms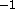
in speed and
0.3--0.8
in direction.
Above the CBL, the RMS errors vary between 0.1--3.0 ms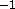
in speed and
1.0--30
in direction, since the correlations get poorer due to
aerosol structures diminishing with altitude and clouds blocking the signal.
The RMS errors decrease as the averaging time interval increases,
since the time averaging of the cross correlation functions
reduces random correlations.
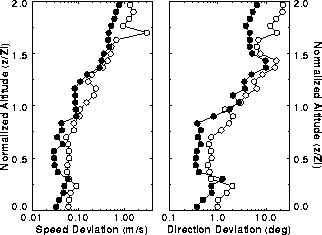
Figure 37:
Root-mean-square error estimate profiles of reliable results
as functions of averaging time interval and normalized altitude
from July 26 to July 31, 1989.
The altitude is normalized with the convective boundary layer mean depth.
Note the logarithmic horizontal axes.
The profiles show RMS errors of wind measurements with
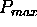= 1 averaged over a 5-hour period.
Errors of 3-minute (open circles)
and hourly averaged (black circles) profiles are shown.
The RMS errors decrease as the averaging time interval increases.
The minimum errors are obtained in the middle of the convective boundary layer.
Below it, turbulent mixing smears the aerosol structures and
decreases the signal-to-noise ratio of the CCF.
Above it, the clouds block part of the data and decrease the signal to
noise ratio.