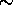 1.
The comparison between expected and measured
detection efficiency values is given in Table 2.
This comparison was made without using the low resolution etalons.
Each etalon decreases the transmission by a factor of
1.
The comparison between expected and measured
detection efficiency values is given in Table 2.
This comparison was made without using the low resolution etalons.
Each etalon decreases the transmission by a factor of 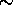 2.
2.



The signal detected with a photon counting system is a combination of backscatter signal, background light, and internal noise in the photodetector. The lidar equation (Eq. (1)) shows that the amount of received signal is determined by the number of transmitted photons, scattering cross section, backscatter phase function, area of the telescope, transmission of the receiver optics, and the sensitivity of the detectors. On the other hand, the HSRL measurements are dependent on the system calibration coefficients (Eqs. (17) and (18)). The errors in the HSRL measurements can be divided into 5 main categories:
The error in the photon counting process is proportional to the square root of the measured signal. The errors due to photon counting statistics that are induced to the calibration coefficients were discussed in Chapter 5.
The system detection efficiency is a combination of the system transmission and the photomultiplier quantum efficiency. The system detection efficiency affects the amount of detected signal and therefore, it is directly related to the photon counting statistics. A model to calculate the expected system transmission was developed. This model includes the spectral transmission of interference filters, etalons, and iodine absorption cell, transmissions and reflections of optical components (lenses, mirrors, cubes, etalon chamber windows) and photomultiplier quantum efficiencies. The transmittance and reflectance values of different optical components were confirmed with measurements. The calculated transmission efficiencies were compared with the measured values. For this study, a clear air case was chosen. Because the properties of molecular scattering are well known, the lidar equation for molecular scattering (Eq. 3) can be solved for the number of photons expected for the pure molecular return.
In
order to predict the expected molecular return, the calculated
system transmission was convoluted with the calculated molecular
spectrum at a 5 km reference altitude. The temperature for
the Doppler-broadened molecular spectrum calculation was
taken from a radiosonde profile.
By calculating the ratio of measured to expected number of
photons given by the lidar equation, the actual system transmission
was estimated. The two way extinction between lidar and
the backscatter volume was assumed to 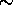 1.
The comparison between expected and measured
detection efficiency values is given in Table 2.
This comparison was made without using the low resolution etalons.
Each etalon decreases the transmission by a factor of
1.
The comparison between expected and measured
detection efficiency values is given in Table 2.
This comparison was made without using the low resolution etalons.
Each etalon decreases the transmission by a factor of  2.
2.
Table 2: HSRL detection efficiency
The transmission efficiency values show  25 % difference
between calculated and measured values. A
25 % difference
between calculated and measured values. A 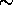 10%
error can be made by assuming the extinction between lidar to 1.
Also the uncertainty on the transmission and reflectance
values of optical components affect the calculation.
The largest uncertainty is the quantum efficiency of the
photomultipliers. The value 0.12 is
taken from the manufacturers specification, but only a 0.03 change
in the quantum efficiency would correct the difference.
The transmissions and reflectances of the receiver components
that affect to the detection efficiency
are listed in Table 3. The transmission and reflection
numbers of some components are confirmed with a measurement and
rest of the values
are obtained from the manufacturers specifications.
10%
error can be made by assuming the extinction between lidar to 1.
Also the uncertainty on the transmission and reflectance
values of optical components affect the calculation.
The largest uncertainty is the quantum efficiency of the
photomultipliers. The value 0.12 is
taken from the manufacturers specification, but only a 0.03 change
in the quantum efficiency would correct the difference.
The transmissions and reflectances of the receiver components
that affect to the detection efficiency
are listed in Table 3. The transmission and reflection
numbers of some components are confirmed with a measurement and
rest of the values
are obtained from the manufacturers specifications.
Table 3: Transmission / Reflection losses in HSRL components. The
source for the transmission and reflection values is manufacturers
specification (spec.) or a measurement (meas.).
The reflectivity of the telescope mirrors is limited
by the reflectivity of the aluminum coating.
The poor transmission values of the etalon chamber windows and the
mirrors have a big effect on the detection efficiency, because they lose
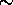 41% of the received signal. These components are
taken from the old system and they are not optimized for
the current operating wavelength. In order to increase the
system performance, these components are going to be replaced in
near future.
41% of the received signal. These components are
taken from the old system and they are not optimized for
the current operating wavelength. In order to increase the
system performance, these components are going to be replaced in
near future.
The errors due to change in the system calibration coefficients are mainly caused by change in the transmission-receiver wavelength tuning and change in the system alignment. These errors can be calculated by a partial differentiation.
A change in atmospheric temperature and pressure affects
the amount of detected molecular signal. Therefore, if the
radiosonde profile is not valid for the measurement conditions,
an error is generated in the calculated molecular signal. The
width of the Doppler-broadened spectrum directly affects
the calibration coefficient 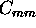 . This affects to
the amount of molecular signal subtracted from the signal
detected with the combined aerosol+molecular channel.
In Brillouin spectrum and molecular backscatter cross section
calculations, the
effects of changing atmospheric conditions are minimized
by using the current radiosonde data from the nearest weather
stations. By comparing temperature and pressure readings
from the closest radiosonde stations,
an
. This affects to
the amount of molecular signal subtracted from the signal
detected with the combined aerosol+molecular channel.
In Brillouin spectrum and molecular backscatter cross section
calculations, the
effects of changing atmospheric conditions are minimized
by using the current radiosonde data from the nearest weather
stations. By comparing temperature and pressure readings
from the closest radiosonde stations,
an 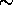 1-5 % difference between
stations is observed. This due to the geographic
separation between weather stations. Because the lidar
is located between these stations, the error is expected to be
smaller.
1-5 % difference between
stations is observed. This due to the geographic
separation between weather stations. Because the lidar
is located between these stations, the error is expected to be
smaller.
In addition to the atmospheric temperature and pressure changes, the effects of the wind on the measurement has to be considered because the high wind velocities can shift the Doppler-broadened spectrum with respect to the laser wavelength. A bulk shift in respect to the radiated spectrum is an indicator of wind, while the line broadening is associated with the random thermal motions of the molecules (and aerosols). If the line center of the Doppler-broadened spectrum is shifted in respect to the transmitted wavelength, the system calibration will be in error. The Doppler-shift for the backscatter signal can be calculated from
where
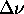 = wavenumber shift
= wavenumber shift
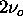 = wavenumber of the laser line center
= wavenumber of the laser line center
v = molecular velocity
c = velocity of light
The wind velocities measured by a radiosonde
can be used as an estimate for the horizontal wind.
The maximum horizontal wind velocities
are generally smaller than 70 m/s at cirrus cloud altitudes, and
the maximum vertical winds are
normally below 1 m/s in troposphere. Therefore, the maximum wind to the
lidar pointing direction 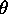 (
(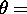 4 degrees from the zenith) is
4 degrees from the zenith) is
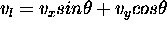 , which corresponds to a
velocity of 5.9 m/s. The shift in the spectrum is 19.8 fm, which
is much smaller than the current 0.052 pm detection accuracy of the molecular
spectrum.
Also the horizontal wind speeds are generally much lower [49],
and therefore, the effects due to wind to the HSRL measurements
are negligible, but caution is required if
larger zenith angles of the pointing direction are considered.
, which corresponds to a
velocity of 5.9 m/s. The shift in the spectrum is 19.8 fm, which
is much smaller than the current 0.052 pm detection accuracy of the molecular
spectrum.
Also the horizontal wind speeds are generally much lower [49],
and therefore, the effects due to wind to the HSRL measurements
are negligible, but caution is required if
larger zenith angles of the pointing direction are considered.
The uncertainty in transmitter-receiver peak transmission tuning can be seen as a shift in the transmitter wavelength in respect to the spectral transmission maximum of the receiver. This effects the amount of detected molecular signal, but if the drift is large, a change in the amount of detected aerosol is observed. The drift also affects the system transmission. In the current HSRL, the effects of a drift between transmitter and receiver wavelengths are minimized by locking the transmitter laser wavelength to the iodine absorption peak (see Chapter 5.2). The effects of the wavelength locking to the measured signal were also discussed in Chapter 5.2.
In addition to the previous errors, the system calibration is affected by all misalignments of the system. The error due to a system misalignment can be divided into three different categories:
A small alignment error (off focus, off axis or misalignment in system pointing direction) can lead situations, where part of the backscattered light is lost in the optics, detector, or atmosphere. This can easily lead into a range dependence of the received signal. This affects the inversion and furthermore, the measured optical depth. A misalignment also affects the total system transmittance and the signal to noise ratio of the measured signal. System pointing instabilities make the overlap correction of the received signal difficult. The overlap region is the close distance range where the overlap of the receiver field of view and the transmitted beam is incomplete. The effect of misalignment between transmitter end receiver pointing directions is largest for the overlap region. The effects vary daily depending from the accuracy of the alignment between transmitter and receiver pointing direction. Large receiver field of views are less critical for the alignment errors. The signal measured with the large field of views of the WFOV channel can be used to align the small field of view channels. In the HSRL, the alignment between transmitter and receiver pointing directions is performed as follows. A corner cube is used to direct the outgoing laser beam to the receiver. The beam is aligned to the center of the receiver aperture by adjusting the turning mirror on the top of the telescope secondary mirror. Then the corner cube is removed and the signal from the atmosphere is used to verify the alignment. The signal of the large field of view of the WFOV-channel is compared to signal of the combined channel. If the channels are properly aligned and if the transmitter and receiver pointing directions are the same, the slopes of the signals are similar for the altitudes above the overlap region and therefore, the ratio between WFOV-channel signal to the spectrometer channel signal is constant. The alignment of the smallest WFOV channel aperture can be verified similarly by comparing the signal from the larger aperture to the signal from the smallest WFOV aperture. The effects of alignment errors on the system measurement accuracy are not included to the error analysis, because with a careful alignment the errors can be minimized.
The accuracy of the background correction is mostly affected by the photon counting statistics. The effects of photon counting on the measured background are decreased by summing at least 66 range bins together. The background correction method used in HSRL measurements was described earlier in Chapter 3.2.2. In addition to the photon counting statistics, the accuracy of the background correction is affected by the slight tendency to overestimate the number of background counts for altitudes close to 33 km. Eventhough atmospheric density, and therefore the amount of Rayleigh scattering, decreases rapidly with the range, some of the signal that is measured into the upper range bins of the HSRL can still be due to Rayleigh scattering. Therefore, when those range bins are used to calculate the number of background counts, the background is slightly overestimated due to the Rayleigh signal.
The effects of the multiple scattering on the received lidar signal are usually neglected and the received signal is assumed to be single scattered. A lidar return from water and thick cirrus clouds usually encounters large optical depths within a short distance of the cloud boundary and therefore, many of the received photons are likely to be from multiple scattering. The effect of multiple scattering to the lidar signal is dependent from the receiver field of view, cloud particle size, range from the lidar, and the optical depth of the cloud. The effect of multiple scattering can be seen in the lidar profile as a reduction in the rate of attenuation of the signal. In depolarization, the effect of multiple scattering will show up as an increase in the depolarization ratio towards the cloud top. The HSRL measurements have shown, that the effect of multiple scattering on the smallest field of view signals is small, because the depolarization ratio values observed for the water clouds are low.
The current HSRL profiles are not corrected for multiple scattering contributions. An inversion program that accounts multiple scattering effects is currently in progress. The magnitude of the error caused by assuming the signal to be originated from single scattering depends from the field of view of the receiver, optical thickness of the cloud, size of the cloud particles, and penetration depth. The clear air aerosols and thin cirrus layers have a small or no multiple scattering effect. Because of the large particle size of ice crystals, the signal from thick cirrus clouds contains a multiple scattering contribution even for the small field of views. The multiple scattering from water cloud droplets is distributed to the larger field of views. The amount of multiple scattering on the measured signal can be estimated from the paper by Eloranta and Shipley [27].