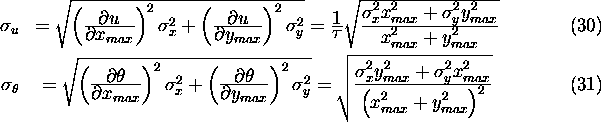


Next: Results and Discussion
Up: Error Analysis
Previous: Random Cross Correlation
Return to the Publications.
Return to the Index.
The wind speed and direction errors are estimated
by calculating the change in the maximum correlation peak position
 when the CCF has additional noise.
In this section, the error of the fit parameters is determined and
then used to estimate the position error of the maximum of the
fitted function.
The expected root-mean-square errors in the wind speed and direction
are derived from the position error.
when the CCF has additional noise.
In this section, the error of the fit parameters is determined and
then used to estimate the position error of the maximum of the
fitted function.
The expected root-mean-square errors in the wind speed and direction
are derived from the position error.
Most of the signal noise in the daytime VIL measurements originates
from the photon noise due to background light.
This leads to spatially uncorrelated noise in the CAPPI scans.
However,
since the histogram equalization of a CAPPI scan
is a highly nonlinear operation, a CCF does not provide enough
information about the spatial distribution of noise.
To make analytical formulation of the noise effects possible,
the noise is assumed uncorrelated with a constant variance.
However, the accuracy of this approximation remains undetermined.
If the noise in the CCF plane is spatially uncorrelated
and the variance of the noise is 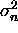 ,
the covariance matrix of the estimated model parameters
,
the covariance matrix of the estimated model parameters 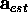 solved from equation (14) is given by
solved from equation (14) is given by
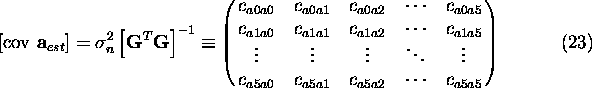
The noise variance 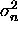 of the CCF is estimated
by the following.
First, an average of three vertically closest CCF planes are
subtracted from the CCF
of the CCF is estimated
by the following.
First, an average of three vertically closest CCF planes are
subtracted from the CCF
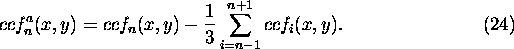
Then, the CCF planes are masked by
rejecting all pixels inside the global maximum correlation region
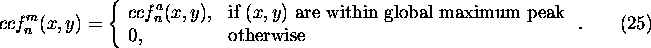
Finally, noise variance 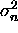 is calculated from the masked CCF
is calculated from the masked CCF
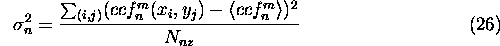
where 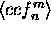 denotes the mean value of the masked
correlation function and
denotes the mean value of the masked
correlation function and 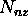 the number of nonzero
elements in the masked correlation function.
the number of nonzero
elements in the masked correlation function.
The mean-squared determination error of the maximum peak position
is given by
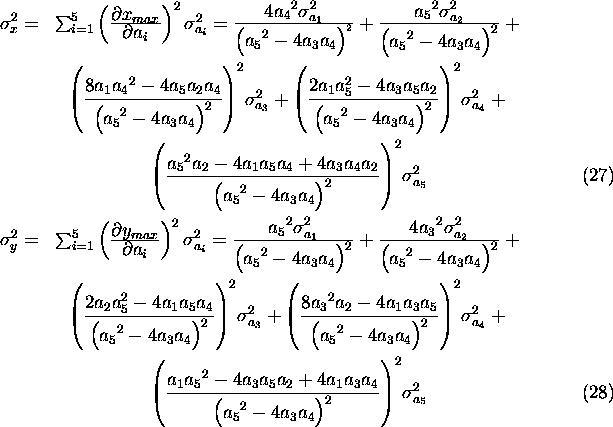
where
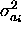 s are error variances of model parameters
s are error variances of model parameters 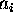 estimated from the model parameter covariance matrix
estimated from the model parameter covariance matrix
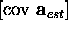 as
as

Finally, the root-mean-square errors 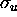 and
and 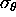 for wind speed and direction estimates, respectively,
are determined from
for wind speed and direction estimates, respectively,
are determined from
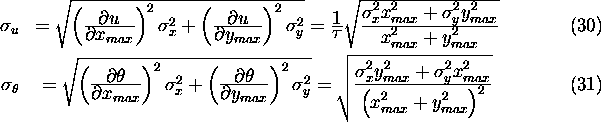
The direction error is expressed in radians.
These equations represent root-mean-square errors of the mean wind estimate
due to a position error of the maximum correlation peak from a noisy CCF.
Since the previous error analysis does not take into account
errors due to possible deformation of aerosol structures between scans,
the errors may be underestimated.
Furthermore, the error variance may be poorly estimated due to
nonlinear effects of the histogram equalization of the CAPPI scans.
Aerosol deformation is expected to become a significant error source
in the presence of gravity waves or strong vertical wind shear.
The gravity waves affect the formation of aerosol structures
by providing an additional energy source.
The aerosol structures tend to follow the wave structure.
Therefore, the aerosol structures move by the group velocity of
the gravity waves, which differs from the velocity of the air mass.
A strong, vertical wind shear may systematically
deform aerosol structures, which may tilt the maximum peak of the
cross correlation function.
The effects of both error sources on the VIL wind profiles
are difficult to examine.
A comprehensive study would
require insitu measurements with an instrument which has similar
averaging properties and accuracy as the VIL, and which also can
directly measure the air mass movements.
Therefore, this problem is not examined further in this study.



Next: Results and Discussion
Up: Error Analysis
Previous: Random Cross Correlation
Return to the Publications.
Return to the Index.
Antti Piironen
Tue Mar 26 20:53:05 CST 1996
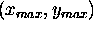 when the CCF has additional noise.
In this section, the error of the fit parameters is determined and
then used to estimate the position error of the maximum of the
fitted function.
The expected root-mean-square errors in the wind speed and direction
are derived from the position error.
when the CCF has additional noise.
In this section, the error of the fit parameters is determined and
then used to estimate the position error of the maximum of the
fitted function.
The expected root-mean-square errors in the wind speed and direction
are derived from the position error.



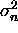 ,
the covariance matrix of the estimated model parameters
,
the covariance matrix of the estimated model parameters 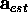 solved from equation (
solved from equation (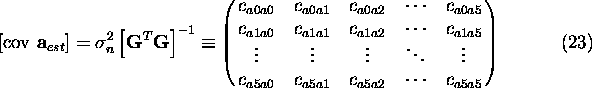
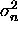 of the CCF is estimated
by the following.
First, an average of three vertically closest CCF planes are
subtracted from the CCF
of the CCF is estimated
by the following.
First, an average of three vertically closest CCF planes are
subtracted from the CCF
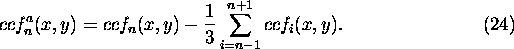
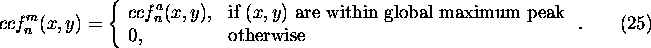
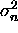 is calculated from the masked CCF
is calculated from the masked CCF
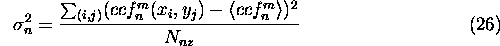
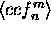 denotes the mean value of the masked
correlation function and
denotes the mean value of the masked
correlation function and 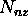 the number of nonzero
elements in the masked correlation function.
the number of nonzero
elements in the masked correlation function.
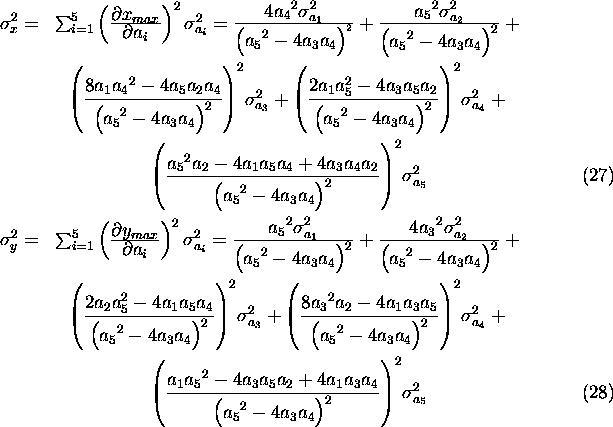
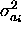 s are error variances of model parameters
s are error variances of model parameters 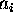 estimated from the model parameter covariance matrix
estimated from the model parameter covariance matrix
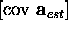 as
as

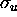 and
and 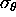 for wind speed and direction estimates, respectively,
are determined from
for wind speed and direction estimates, respectively,
are determined from