Next: About this document
Previous: Conference papers
Presented at the Conference on Lasers and Electro-Optics, Aug 30-Sept 3,
Seoul, Korea
Lidar Measurements of Vector Wind Fields
E. W. Eloranta, S. D. Mayor, and J. P. Garcia
Univerisity of Wisconsin-Madison
Madison, WI 53706
tel: 608-262-7327, fax 608-262-5974
eloranta@lidar.ssec.wisc.edu
Introduction
In this paper, both horizontal components of the wind vector are
measured with 250 m spatial resolution over a 6 by 10 km area. These
are derived using 2-dimensional cross-correlations computed between a
series of aerosol backscatter images recorded with the University of
Wisconsin Volume Imaging Lidar (VIL).
The VIL is designed to provide high spatial and temporal resolution
images of atmospheric structure. It employs a 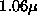 m laser operating
at a repetition rate of 100 Hz, 0.5-m diameter scanning optics, and a
fast data acquisition system to generate two- and three-dimensional
images. Under typical conditions, the system records data to a range of 18
km with a range resolution of 15 m. The data system records profiles
without averaging. Approximately 1 G-byte of data is recorded per hour
of operation.
m laser operating
at a repetition rate of 100 Hz, 0.5-m diameter scanning optics, and a
fast data acquisition system to generate two- and three-dimensional
images. Under typical conditions, the system records data to a range of 18
km with a range resolution of 15 m. The data system records profiles
without averaging. Approximately 1 G-byte of data is recorded per hour
of operation.
This paper analyzes repeated azimuthal scans made with
the lidar elevation angle set near zero. A typical scan covered an
azimuthal sector of 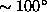 and provided lidar profiles at
and provided lidar profiles at
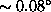 increments. The full back-and-forth scan was
repeated at
increments. The full back-and-forth scan was
repeated at 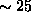 s intervals.
s intervals.
Wind Calculations
We have previously developed algorithms to measure vertical profiles
of the horizontal wind from a series of volumetric lidar images of
aerosol structure (Schols and Eloranta 1992, Piironen and Eloranta,
1995). These provide a single wind vector for each altitude
representing the mean wind averaged over the 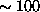 km
km area of
a typical scan. In this paper, these algorithms are modified to
provide a vector wind field with a 250 m spatial resolution.
Correlations are computed between square image segments which are 250
meters on a side. Correlations are computed between every other scan so
that left-moving and right-moving scans are always paired with the
same scan direction and thus the time interval between laser profiles
in each part of successive images is
area of
a typical scan. In this paper, these algorithms are modified to
provide a vector wind field with a 250 m spatial resolution.
Correlations are computed between square image segments which are 250
meters on a side. Correlations are computed between every other scan so
that left-moving and right-moving scans are always paired with the
same scan direction and thus the time interval between laser profiles
in each part of successive images is 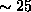 s. Because the
winds were as large as 9 m/s, the wind advected aerosol structures by up to
225 m between scans. This created noise in the cross correlation
calculation because most of the structure seen in the first image was
advected out of the image area before the next scan. To
minimize this problem, the second image in each correlation pair is
selected from a position displaced downwind of the first image by the
distance the structure is expected to move between scans. This allows
the correlation to take place with approximately the same air mass
that was present in the first image. The displacement of the image
position is added to the displacement of the correlation peak to
compute the wind vector. The a priori wind vector required to compute
the displacement of the second image is computed by first generating a
wind field with 500 m spatial resolution where the advection distance
is a smaller fraction of the image size.
s. Because the
winds were as large as 9 m/s, the wind advected aerosol structures by up to
225 m between scans. This created noise in the cross correlation
calculation because most of the structure seen in the first image was
advected out of the image area before the next scan. To
minimize this problem, the second image in each correlation pair is
selected from a position displaced downwind of the first image by the
distance the structure is expected to move between scans. This allows
the correlation to take place with approximately the same air mass
that was present in the first image. The displacement of the image
position is added to the displacement of the correlation peak to
compute the wind vector. The a priori wind vector required to compute
the displacement of the second image is computed by first generating a
wind field with 500 m spatial resolution where the advection distance
is a smaller fraction of the image size.
Figure 1 shows the wind field computed from data acquired 5 m above
the surface of Lake Michigan as cold air (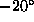 C) passed over
C) passed over
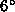 C water. Figure 2, which presents North-South averages,
shows the acceleration and veering of the wind as it leaves the shore.
The wind shadow in the lee of the coastline is clearly visible. A
careful examination of figure 1 shows that the wind shadow length
varies with position. This reflects variations in the topography and
surface roughness along the shore. The error bars in figure 2 were
computed from the variance of the values contributing to each
north-south average; with the errors set equal to the square-root of
the variance divided by the square root of the number of points
contributing to the average (24 points in this case). These tend to
underestimate the true error by failing to include systematic errors
while at the same time tending to overestimate the errors because the
true geophysical variability is included in the calculated
variance. The estimated errors in the North-South average wind speed
and direction are
C water. Figure 2, which presents North-South averages,
shows the acceleration and veering of the wind as it leaves the shore.
The wind shadow in the lee of the coastline is clearly visible. A
careful examination of figure 1 shows that the wind shadow length
varies with position. This reflects variations in the topography and
surface roughness along the shore. The error bars in figure 2 were
computed from the variance of the values contributing to each
north-south average; with the errors set equal to the square-root of
the variance divided by the square root of the number of points
contributing to the average (24 points in this case). These tend to
underestimate the true error by failing to include systematic errors
while at the same time tending to overestimate the errors because the
true geophysical variability is included in the calculated
variance. The estimated errors in the North-South average wind speed
and direction are 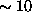 cm/s and
cm/s and 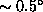 respectively,
while for the individual wind measurements shown in figure 1, the
estimated errors are
respectively,
while for the individual wind measurements shown in figure 1, the
estimated errors are 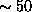 cm/s and
cm/s and 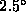 for the speed and
velocity respectively.
for the speed and
velocity respectively.
This paper will also present divergence and vorticity fields computed
from the vector winds.
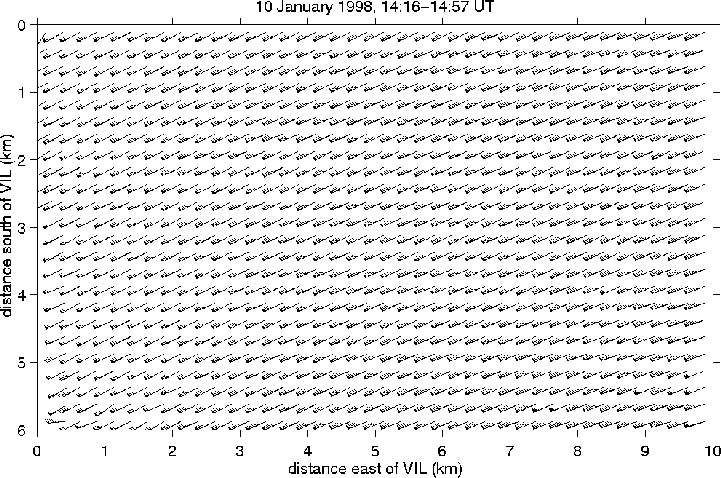
Figure 1. Wind vectors computed from 240 PPI scans 5 m
above lake Michigan during a cold air outbreak between 14:15 and 14:57
UT on January 10, 1998. The shore line roughly parallels the left edge
of the figure. Meteorological wind barbs are presented with single
barbs and triangles indicating 1 m/s and 5 m/s respectively.
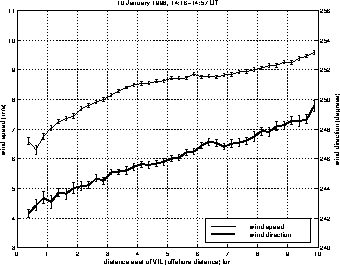
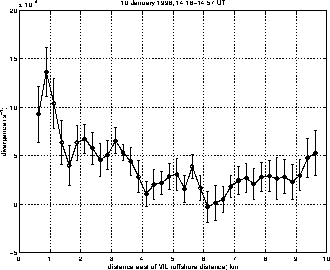
Figure 2. Average wind speed, direction (left-panel) and
divergence (right-panel) as a function of distance from the shore
between 14:15 and 14:57 UT on January 10, 1998. The acceleration and
veering of the wind with offshore distance are clearly seen. This plot
is computed from a north-south averaging of the data shown in figure
1.
References
- Schols, J. L., and E. W. Eloranta, 1992: The calculation of area-averaged
vertical profiles of the horizontal wind velocity from volume imaging
lidar data ., J. of Geophys. Res., 97, 18395-18407.
- Piironen, A. and E. W. Eloranta, 1995: An accuracy analysis of the
wind profiles calculated from Volume Imaging Lidar data,
J. of Geophys. Res., 100, 25559-25567.
Next: About this document
Previous: Conference
papers
Ed Eloranta
Mon Nov 15 17:15:24 CST 1999
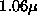 m laser operating
at a repetition rate of 100 Hz, 0.5-m diameter scanning optics, and a
fast data acquisition system to generate two- and three-dimensional
images. Under typical conditions, the system records data to a range of 18
km with a range resolution of 15 m. The data system records profiles
without averaging. Approximately 1 G-byte of data is recorded per hour
of operation.
m laser operating
at a repetition rate of 100 Hz, 0.5-m diameter scanning optics, and a
fast data acquisition system to generate two- and three-dimensional
images. Under typical conditions, the system records data to a range of 18
km with a range resolution of 15 m. The data system records profiles
without averaging. Approximately 1 G-byte of data is recorded per hour
of operation.
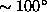 and provided lidar profiles at
and provided lidar profiles at
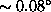 increments. The full back-and-forth scan was
repeated at
increments. The full back-and-forth scan was
repeated at 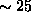 s intervals.
s intervals.
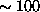 km
km area of
a typical scan. In this paper, these algorithms are modified to
provide a vector wind field with a 250 m spatial resolution.
Correlations are computed between square image segments which are 250
meters on a side. Correlations are computed between every other scan so
that left-moving and right-moving scans are always paired with the
same scan direction and thus the time interval between laser profiles
in each part of successive images is
area of
a typical scan. In this paper, these algorithms are modified to
provide a vector wind field with a 250 m spatial resolution.
Correlations are computed between square image segments which are 250
meters on a side. Correlations are computed between every other scan so
that left-moving and right-moving scans are always paired with the
same scan direction and thus the time interval between laser profiles
in each part of successive images is 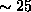 s. Because the
winds were as large as 9 m/s, the wind advected aerosol structures by up to
225 m between scans. This created noise in the cross correlation
calculation because most of the structure seen in the first image was
advected out of the image area before the next scan. To
minimize this problem, the second image in each correlation pair is
selected from a position displaced downwind of the first image by the
distance the structure is expected to move between scans. This allows
the correlation to take place with approximately the same air mass
that was present in the first image. The displacement of the image
position is added to the displacement of the correlation peak to
compute the wind vector. The a priori wind vector required to compute
the displacement of the second image is computed by first generating a
wind field with 500 m spatial resolution where the advection distance
is a smaller fraction of the image size.
s. Because the
winds were as large as 9 m/s, the wind advected aerosol structures by up to
225 m between scans. This created noise in the cross correlation
calculation because most of the structure seen in the first image was
advected out of the image area before the next scan. To
minimize this problem, the second image in each correlation pair is
selected from a position displaced downwind of the first image by the
distance the structure is expected to move between scans. This allows
the correlation to take place with approximately the same air mass
that was present in the first image. The displacement of the image
position is added to the displacement of the correlation peak to
compute the wind vector. The a priori wind vector required to compute
the displacement of the second image is computed by first generating a
wind field with 500 m spatial resolution where the advection distance
is a smaller fraction of the image size.
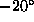 C) passed over
C) passed over
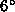 C water. Figure 2, which presents North-South averages,
shows the acceleration and veering of the wind as it leaves the shore.
The wind shadow in the lee of the coastline is clearly visible. A
careful examination of figure 1 shows that the wind shadow length
varies with position. This reflects variations in the topography and
surface roughness along the shore. The error bars in figure 2 were
computed from the variance of the values contributing to each
north-south average; with the errors set equal to the square-root of
the variance divided by the square root of the number of points
contributing to the average (24 points in this case). These tend to
underestimate the true error by failing to include systematic errors
while at the same time tending to overestimate the errors because the
true geophysical variability is included in the calculated
variance. The estimated errors in the North-South average wind speed
and direction are
C water. Figure 2, which presents North-South averages,
shows the acceleration and veering of the wind as it leaves the shore.
The wind shadow in the lee of the coastline is clearly visible. A
careful examination of figure 1 shows that the wind shadow length
varies with position. This reflects variations in the topography and
surface roughness along the shore. The error bars in figure 2 were
computed from the variance of the values contributing to each
north-south average; with the errors set equal to the square-root of
the variance divided by the square root of the number of points
contributing to the average (24 points in this case). These tend to
underestimate the true error by failing to include systematic errors
while at the same time tending to overestimate the errors because the
true geophysical variability is included in the calculated
variance. The estimated errors in the North-South average wind speed
and direction are 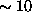 cm/s and
cm/s and 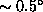 respectively,
while for the individual wind measurements shown in figure 1, the
estimated errors are
respectively,
while for the individual wind measurements shown in figure 1, the
estimated errors are 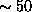 cm/s and
cm/s and 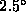 for the speed and
velocity respectively.
for the speed and
velocity respectively.


